Conformità al limite di legge

Criterio decisionale per la conformità al limite di legge

L’articolo con titolo “conformità al limite di legge” è stato redatto seguendo il contenuto del documento: “Ispra, L’analisi di conformità con i valori di legge: il ruolo dell’incertezza associata a risultati di misura, Manuali e linee guida 52/2009”,

L’incertezza di misura associata al risultato analitico fornisce uno strumento per la valutazione di conformità, nei casi in cui la norma di riferimento non dia indicazioni sulle regole decisionali da adottare. 

Siano: R la miglior stima del valore della proprietà d’interesse e VL l’estremo superiore dell’intervallo di accettazione stabilito dalla normativa.

La valutazione di conformità ad un limite di legge avviene confrontando l’intervallo di accettazione con l’intervallo costituito dall’incertezza associata alla migliore stima del “valore vero” della proprietà d’interesse.

Sulla base di questo confronto, si possono prendere le seguenti decisioni:

• la matrice è conforme, nel seguito definito “NON non conforme”, oppure
• la matrice è “non conforme”.

Criterio ed applicazioni per la conformità al limite di legge

Con questo criterio è possibile effettuare la valutazione dei risultati e gli adempimenti di legge nel caso in cui i rapporti di prova (RdP) emessi dai Laboratori forniscono un risultato analitico (R ) corredato del valore dell’incertezza di misura (U_RdP) superiore, o comunque in prossimità, del valore limite di legge (VL).

Il criterio si applica ai risultati delle analisi effettuate per valutare la conformità al limite di legge cioè a un VL (valore limite), inteso come valore massimo accettabile stabilito da norme di legge, nei casi in cui la legislazione di riferimento non dia precise indicazioni inerenti le modalità di valutazione di conformità.

Si applica ad analisi/misure puntuali il cui risultato è espresso in valore di concentrazione, nelle unità di misura direttamente confrontabili con i valori limite espressi dalla legislazione vigente. 

Non si applica a valori medi o percentili di serie di dati, né a valori assoluti di analiti.

Il criterio non si applica nei casi in cui la legislazione di riferimento o l’atto autorizzativo stesso fornisca precise indicazioni cogenti inerenti le modalità di valutazione della conformità a un VL.

Incertezza

L’incertezza estesa di misura riportata in un RdP individua un intervallo di confidenza all’interno del quale cade il risultato della misurazione con una definita probabilità, che deve essere dichiarata sul RdP stesso (di norma del 95%).

L’incertezza estesa è definita come:

U_RdP = K_0.95 * u_c (1)

dove: 

• K_0.95 = fattore di copertura al 95% (= t di Student)
• u_c = incertezza composta

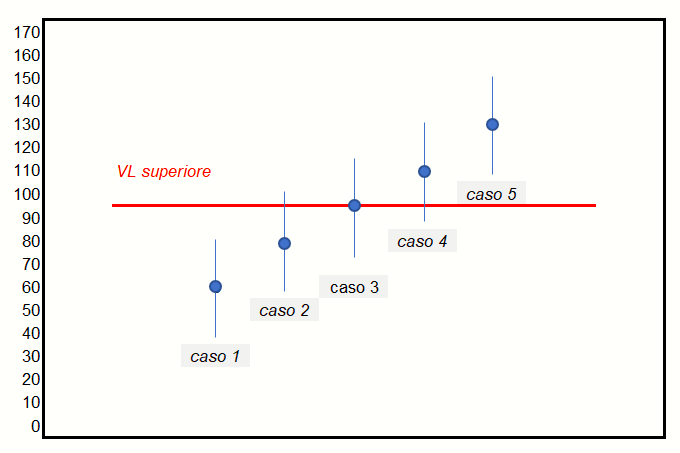
Figura 1: rappresentazione grafica di possibili casistiche

Possibili casistiche

Nel confronto di un risultato con un valore limite si possono verificare 5 casi (vedi figura 1).

Solo per il caso 3 sarà necessario definire una regola decisionale.

Infatti, come si vede dalla figura e come è documentato nel MLG 52/09 ISPRA il caso:

• 1: rappresenta una situazione di rispetto del valore limite VL; 
• 5: situazione di non conformità per risultato superiore al VL;
• 3: costituisce una situazione di rispetto del valore limite VL in quanto coincidente con il VL;
• 2: rientra anch’esso tra le situazioni di rispetto del VL, in quanto la probabilità che il risultato della misurazione si collochi nella porzione di intervallo di confidenza superiore al VL è percentualmente inferiore alla probabilità che il risultato si collochi nella porzione di intervallo di confidenza inferiore al VL. La probabilità di superamento infatti sarebbe inferiore al 50%, e quindi di molto inferiore al 95% necessario a definire la certezza statistica del dato.

Per dirimere situazioni con risultato riconducibile al caso 4, si fa riferimento al MLG 52/2009 [1] che prevede un approccio probabilistico al fine di stabilire statisticamente la significatività del superamento: si considera il Risultato (R ) della misura “non conforme” quando risulta maggiore del VL con probabilità > 95% (oltre ogni ragionevole dubbio).

Modalità di calcolo

Per l’applicazione di questa regola è necessaria la ridefinizione dell’intervallo di confidenza determinato dall’incertezza di misura espressa sul RdP, passando da un fattore di copertura di tipo bilaterale a quello di tipo unilaterale e definendo una “guard band (g)”, che individua il nuovo intervallo di confidenza:

g = K’_0.95 * u_c (2)

Per il calcolo della “guard band” a partire dall’incertezza di misura dichiarata nel rapporto di prova, si procede nel modo seguente:

u_c = U_RdP/K = U_RdP/2 (3)

pertanto:

g = K’_0.95 * U_RdP/K = 1,645 * U_RdP/2 = 0,82 * U_RdP (4)

Per un valore di probabilità del 95% il valore di K’_0.95 per una distribuzione normale è 1,645, quindi la dimensione della band guard sarà 1.645 * u_c.

Casistica

Se la U_RdP è solo di tipo analitico e nella stima dell’incertezza rientrano ulteriori contributi relativi all’incertezza di campionamento (u_{campionamento}), in funzione delle definizioni di misurando e di VL previsto dalle norme di riferimento, si procede nel seguente modo:

1) stima dell’incertezza tipo composta (u_c) secondo l’espressione:

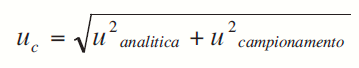
2) stima del numero dei gradi di libertà effettivi (ν_eff) con la formula di Welch-Satterthwaite in particolare quando i contributi in u_c sono approssimativamente della stessa grandezza ed ognuno con numero di gradi di libertà piccolo (≤10). L’espressione della formula di Welch-Satterthwaite è la seguente:

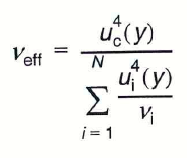
dove:

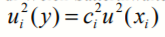
Per un esempio applicativo fare riferimento al documento Linee guida per il calcolo dell’incertezza di misura, Esempi applicativi documento realizzato dalle Agenzie Ambientali.

3) calcolo della “guard band” con l’espressione:

g = K’_0.95 * u_c (5)

Dove il fattore K’_0.95 è calcolabile con le seguenti modalità:

a) se il numero dei gradi di libertà effettivi è “grande” (>10)

K’_0.95 = 1.645 (6)

b) se il numero dei gradi di libertà effettivi è “piccolo” (≤ 10)

il valore del rapporto K’_0.95/K si allontana da 0,82 e sarà cura del Laboratorio indicare il nuovo valore di K’_0.95/K da utilizzare per il calcolo di g (guard band):

K’_0.95 = t_0.95(v) (7)

con: t_{0.95 (veff)} =”t” student unilaterale corrispondente ai v_eff gradi di libertà effettivi e 95 % della distribuzione. Tale valore viene valutato nella tabella del t di Student in funzione dei gradi di libertà.

Facciamo un esempio applicativo con gradi di libertà v<10 tratti dalla tabella del t di Student:

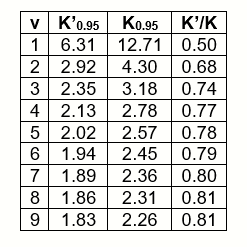
Il laboratorio ha determinato l’incertezza per ν = 6.

Sul RdP dovrà essere dichiarato un valore di K= 2,45: “L’incertezza di misura è calcolata con P=95% e K=2,45”

Dalla tabella si ricava il valore di K’/K = 0,79: tale valore sarà riportato in una nota in calce al RdP.

Si ricava:                                           

g = 0,79 * U_RdP (8)

Regola decisionale

Una volta calcolato il valore di g è possibile definire la “non conformità” del risultato analitico (R) rispetto al limite VL, in base alla seguente relazione: 

R – g ≤ VL  (9)

Se viene soddisfatta la relazione non è possibile stabilire, oltre ogni ragionevole dubbio, la non conformità rispetto al VL, con una probabilità > 95%.

Il VL potrà essere considerato “raggiunto” e di questo potrà essere fornito commento nel rapporto di prova, ad esempio, con l’espressione:

“Il valore misurato, tenuto conto dell’incertezza, non risulta significativamente maggiore del VL, al livello di confidenza del 95%”.

In generale se non diversamente indicato nella norma tecnica di riferimento, i risultati delle misure (R ), con le relative cifre decimali e le incertezze associate U espresse con le idonee cifre significative, devono essere riportati nel rapporto di prova coerentemente con le  caratteristiche espresse nel metodo/procedura di prova.

Cifre significative

Il documento EA-4/16 [2] al punto 7.6 riporta:

“Il numero di cifre decimali in una incertezza riportata deve sempre riflettere la pratica capacità della tecnica di misura. Con riguardo al processo di valutazione delle incertezze, è

raramente giustificato riportare più di due cifre significative. Spesso una sola cifra significativa è appropriata. In analogia, il valore numerico del risultato deve essere arrotondato in modo che l’ultima cifra decimale corrisponda all’ultima cifra (decimale) dell’incertezza. Le normali regole dell’arrotondamento possono essere applicate in entrambi i casi. 

Per esempio, se è ottenuto un risultato di 123,456 unità, ed è risultata dalla stima una incertezza di 2,27 unità, l’uso di due cifre significative porterebbe ai valori arrotondati di 123,5 ± 2,3 unità”.

Se non diversamente indicato nella norma di Legge o in sue interpretazioni, nell’analisi di conformità, i VL devono essere considerati con il numero di cifre decimali con il quale sono espressi nella norma di Legge.

Quindi, quando vale l’espressione:

(R-VL)_arr < 0 (10)

dove viene indicato: 

(R-VL)_arr = la differenza tra il Risultato della misura ed il Valore Limite arrotondata con lo stesso numero di cifre decimali utilizzate dal Normatore nell’espressione del VL.

a prescindere dalla dimensione dell’incertezza della misura, si dovrà concludere che R non eccede il VL perché R si trova all’interno della zona di accettabilità definita, di fatto, dal Normatore con la scelta delle modalità di espressione del VL.

In particolare, quando vale l’espressione:

(R-VL)_arr = 0 (11)

il VL potrà essere considerato “raggiunto” e di questo potrà essere fornito commento, ad esempio, con l’espressione: 

“Il valore misurato, stante le modalità di espressione del VL, non risulta diverso dallo stesso VL”.

Modalità di arrotondamento

L’arrotondamento della differenza (R-VL) al numero di decimali del VL è da effettuare secondo le consuete regole di approssimazione matematica.

Si suggerisce l’utilizzo del metodo di arrotondamento descritto in EPA-SI100 [3] nel seguente modo: “Se il valore del la prima cifra da scartare è inferiore a 5, lascia la cifra da tenere senza nessun cambiamento.

Se il valore della prima cifra da scartare è pari a 5 o maggiore, aumenta di una unità il valore della cifra da tenere”. Tale modalità di arrotondamento è quella normalmente più utilizzata nei programmi informatici di calcolo.

Si riportano alcuni esempi di approssimazione:

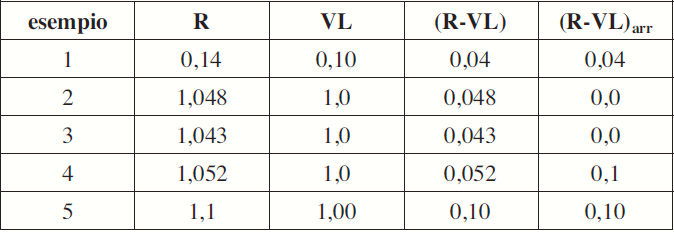
Se valgono contemporaneamente le equazioni: 

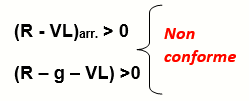
(R – VL)_arr > 0 (11)

(R – g – VL) >0 (12)

si può concludere che il misurando è maggiore del VL con una probabilità maggiore del 95%.

Se valgono contemporaneamente le equazioni riportate si potrà stabilire la non conformità

del campione al quale si riferisce il risultato della misura.

Il MLG Ispra 52/09 ISPRA riporta esempi applicativi a cui si rimanda.

Per approfondimenti sugli argomenti consultare i siti internet riportati nella sezione “Per saperne di più” e dalla norme di riferimento.

Norme di riferimento

• UNI CEI EN ISO/IEC 17025:2018 Requisiti generali per la competenza dei laboratori di prova e taratura
• ILAC-G8:03/2009 – Guidelines on the Reporting of Compliance with Specification
• September 2008, JCGM 100:2008 GUM 1995 with minor corrections Evaluation of measurement data — Guide to the expression of uncertainty in measurement
• UNI CEI 70098-3 Incertezza di misura – Parte 3: guida all’espressione dell’incertezza di misura, settembre 2016

Per saperne di più

Bibliografia

[1] Ispra, L’analisi di conformità con i valori di legge: il ruolo dell’incertezza associata a risultati di misura, Manuali e linee guida 52/2009

[2] EA/4-16 – EA Guidelines on the expression of uncertainty in quantitative testing – december 2003

[3] EPA – SI:100 Mathematics Review for Air Pollution Control Lesson 2: Significant Figures and Rounding Off. (rev 1.0 – 6/3/94)

[4] ILAC-G8:03/2009 – Guidelines on the Reporting of Compliance with Specification

Autore: M.Morelli

aggiornamento del 22/09/2020